A specific study was conducted from POLDER1/ADEOS1 data to define the best set of particle modes (see phase function)
We assume that each mode of spherical particle follows a lognormal distribution,
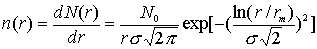
where N0 is the density number,  the standard deviation and rm the modal radius.
the standard deviation and rm the modal radius.
For the small mode, we assume that  = 0.46 , a set of four modal radii rm, from 0.04 to 0.13 µm and the real refractive indices (m = 1.35, 1.45 and 1.60).
= 0.46 , a set of four modal radii rm, from 0.04 to 0.13 µm and the real refractive indices (m = 1.35, 1.45 and 1.60).
For the large mode of spherical particles, we assume that  = 0.69, a modal radius rm = 0.75 µm and three real refractive indices (m = 1.33, 1.35 and 1.37).
= 0.69, a modal radius rm = 0.75 µm and three real refractive indices (m = 1.33, 1.35 and 1.37).
The mode of large non-spherical particles is the mean model given in Volten et al. (2001).
Reference : Volten H., Muñoz O., Rol E., de Haan J.F., Vassen W., and Hovenier J.W.
Scattering matrices of mineral aerosol particles at 441.6 nm and 632.8 nm.
J. Geophys. Res., 106, 17,375-17,401, 2001.
Phase function
Because the C.P.U. time increases with the mode number, it is not possible to introduce a very large set of particle modes to cover the aerosol variability. On the other hand, it is necessary to take into account the most representative modes of particles. With this aim in view, the aerosol phase functions are extracted in the 865 and 670 channels from POLDER. We make this extraction over homogeneous areas (about 100×100 km2) for different aerosol types when measurements cover a large range of scattering angles out of the sunglint (west part of the images).
In a given channel and in a viewing direction, the radiances and the polarized radiances at the top of the atmosphere can be decomposed as follows:
Lmeasured = [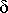 p(
p(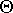 )] /4cos
)] /4cos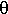 v +
v + 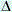 L for the radiance
L for the radiance
Lpmeasured = [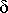 q(
q(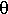
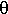 v +
v + 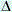 Lp for the polarized radiance
Lp for the polarized radiance
where 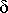 (aerosol optical thickness), p (
(aerosol optical thickness), p (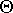 ) (phase function depending on the scattering angle
) (phase function depending on the scattering angle 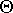 ) and q (
) and q (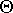 ) (polarized phase function) are relative to the unknown aerosols. The terms
) (polarized phase function) are relative to the unknown aerosols. The terms 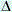 L and
L and 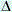 Lp take into account the multiple scattering, the molecular and the surface contributions, and their interactions. The way to estimate
Lp take into account the multiple scattering, the molecular and the surface contributions, and their interactions. The way to estimate 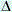 L and
L and 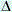 Lp consists to apply the aerosol POLDER algorithm to the measurements and then to simulate the radiances Lsimulated and Lpsimulated using the derived aerosol characteristics, indicated with an asterisk in the following formulas:
Lp consists to apply the aerosol POLDER algorithm to the measurements and then to simulate the radiances Lsimulated and Lpsimulated using the derived aerosol characteristics, indicated with an asterisk in the following formulas:
Lsimulated = 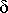 * p*(
* p*(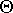 )/4cos
)/4cos 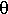
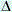 L* for the radiance
L* for the radiance
Lpsimulated = 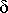 * q*(
* q*(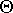 )/4cos
)/4cos 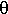 v +
v + 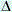 L*p for the polarized radiance
L*p for the polarized radiance
If the derived aerosol characteristics are close to the real ones, we assume 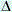 L =
L = 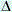 L* and
L* and 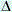 Lp =
Lp = 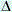 L*p , so the real aerosol contributions are written:
L*p , so the real aerosol contributions are written:
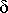 p(
p(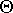 ) =
) = 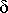 * p*(
* p*(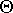 ) + 4cos
) + 4cos 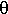 v [Lmeasured – Lsimulated ]
v [Lmeasured – Lsimulated ]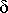 q(
q(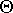 ) =
) = 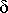 * q*(
* q*(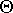 ) + 4cos
) + 4cos 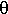 v [Lpmeasured – Lpsimulated ]
v [Lpmeasured – Lpsimulated ]
So, it is easy to deduce the aerosol characteristics (effective radii and refractive indices of the small and large modes) using a large set of phase functions of spherical particles (Mie theory) or non-spherical one. A statistic analysis allows detecting the most useful modes and to improve the basis of models used in the algorithm.
